提案手法とその結果
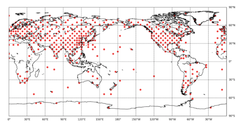
世界におけるラジオゾンデ観測地点

提案手法の概念図

Lorenz 96 モデルの挙動、および提案手法による最新時刻での全状態変数を推定した結果
気象予測の精度向上には二つの要素があります。一つ目は気象シミュレーション自体の精度向上、二つ目は気象シミュレーションと実世界の大気状態を同期するしくみの精度向上です。今回は二つ目に着目して脳のしくみを取り入れました。
気象シミュレーションと実世界の同期を難しくする一つの要因は、得られるセンサ観測値(例:ラジオゾンデと呼ばれるゴム気球による各高度での大気状態の観測)が空間的に疎らであることです(図1参照)。そのため、従来手法では十分に同期させることができず、気象予測の精度低下の一要因となっていました。
そこに、脳のしくみ(例:疎らにしか存在しない皮膚の圧覚センサから得た時間振動等の情報より、指に触れるモノの質感を高精度に感じ取る)を取り入れることで、外界と気象シミュレーションの同期精度の向上を図りました。具体的には、疎らなセンサ情報の時間履歴から、AI技術の一翼を担う深層学習(脳の神経学習機構を工学的に実装したもの)を用いて非観測地点における大気状態を推測します。本提案手法を気象シミュレーションの原理モデルに適用したところ、従来手法に対して大幅な同期精度の向上がみられました。今後は実際の気象予測モデルに適用し性能検証を本格化させていくとともに、日本が高い世界シェアを誇るセンサと掛け合わせたデジタルツイン構想を加速してまいります。(詳細は5. にて後述)
※1 デジタルの仮想空間上に、現実世界の双子(ツイン)を構築したもの
画像1: https://www.atpress.ne.jp/releases/210287/LL_img_210287_2.png
世界におけるラジオゾンデ観測地点
図1 世界におけるラジオゾンデ観測地点:信頼性高く、各高度での気温、圧力、風速等を得るために用いられるラジオゾンデ観測(ゴム気球による大気観測)は、気象シミュレーションの計算グリッド(数km~数10km)に対して疎らである。
1. 社会的背景
持続可能な開発目標(SDGs)「13. 気候変動に具体的な対策を」としても掲げられているように、昨今世界的に発生する気候関連災害や自然災害に対する強靭性(レジリエンス)及び適応力の強化への対応が急務となっています。加えて日本では、台風による洪水やゲリラ豪雨等の頻発で大きな被害により甚大な経済損失が発生しています。各国で盛んに研究開発が行われるなか、日本では防災立国に向けて気象予測の大幅な精度向上が求められています。
2. 現状・技術的課題
現在の気象予測は、気象現象をモデル化した気象シミュレーションを解くことによって行なわれています。その精度向上には二つの要素があり、一つ目は気象シミュレーション自体の精度向上、二つ目はその気象シミュレーションと実世界を同期するしくみの精度向上です。二つ目をデータ同化と呼び、今回はこちらに着目をしています。
一般に、観測気球やアメダスなどの、現実世界の情報を得るための気象観測センサは空間的に疎らにしか存在しておらず、観測データを万遍なく取得することは困難です。そのため、部分的な観測データから実世界の状態を推定する必要があり、アンサンブルカルマンフィルタや三次元変分法、四次元変分法(※2)といったデータ同化手法が研究開発されてきました。これらの手法は、非線形性が高い条件において観測地点が疎らとなる場合や、状態変数が非正規分布となる条件において、データ同化の精度に課題を残していました。
※2 時系列でシミュレーションの値と観測値との差を見ていった後に、その差を減らすための評価関数に基づき、シミュレーションの初期値を更新していく手法。
3. 提案手法
そこで当社では、強い非線形性を有する気象予測のデータ同化精度を高める方法として、AI技術の一種である深層学習を取り入れた手法を開発しました。
具体的には、部分的に観測されたデータの時間履歴を入力とし、最新時刻における全状態変数を教師信号として、その関係性を深層学習によりマッピングしました(図2参照)。また、観測データに含まれるセンサノイズに対応できるように、訓練用データにノイズを加えて訓練を行なっています。
本マッピングの妥当性は、部分観測される一部の状態変数の時間履歴から、現時刻における全状態変数の推測が可能であることを示すTakensの埋め込み定理によって担保されています。
画像2: https://www.atpress.ne.jp/releases/210287/LL_img_210287_3.png
提案手法の概念図
図2 提案手法の概念図:(a)3変数の時系列データ(Lorenz 63モデル)(b)左図:数値シミュレーションの全状態変数によるアトラクタ。右図:時間遅れ座標系と呼ばれる観測時間をτ毎にずらした座標系におけるアトラクタ。提案手法では部分観測空間内のアトラクタから(右図)から、全状態空間内のアトラクタ(左図)へのマッピング関数を獲得するために深層学習を用いる。
4. 検証結果
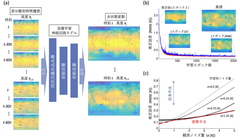
提案手法によるデータ同化精度を検証するため、簡易大気大循環モデルとしてよく用いられるSPEEDYモデル(Simplified Parameterizations primitivE-Equation Dynamics)を対象とし、従来手法との比較を行いました。同一の部分観測条件において、同化の推定誤差が1/3ほどに改善されていることがわかります(図3c)。
画像3: https://www.atpress.ne.jp/releases/210287/LL_img_210287_1.png
提案手法とその結果
図3 提案手法とその結果:(a)SPEEDYモデルの気温のみに対して、現時刻の全状態変数(空間グリッド:地上高x緯度x経度=8x48x96)を、部分観測(空間グリッド:地上高x緯度x経度=8x11x24となるように均等に間引いたもの)の時間履歴(τ=6時間ごとに60ステップまで遡る)から推定する深層学習モデル (b) 逆誤差伝播学習の時間発展。トレーニングデータセット(赤線)とバリデーションデータセット(青線)のそれぞれについて真値との誤差を平均平方二乗誤差(RMSE)を用いて図示している (c) 提案手法(学習後モデル)と従来手法による推定結果の比較。提案手法では部分観測に含まれるガウシアンノイズの大きさを振っており、複数の誤差性能曲線は学習時のノイズ量が異なるもの。
学習時のノイズ量の増加に伴ってより観測ノイズ量に対する頑健性が向上する。図に示した従来手法による推定誤差は近年の論文から引用したものであり、同一の部分観測条件において、単一の観測ノイズ量(σ=1[K])に対してアンサンブルカルマンフィルタ法を用いたもの[1,2,3]
深層学習に用いたモデルは、第一層を四次元の畳み込み層(フィルタサイズ:緯度方向x経度方向x地上高x時間:7x7x3x3)、それ以降を全結合の神経回路網(ニューロン数:21384→7000→7000→36864[8x48x96])であり(図3a)、逆誤差伝播学習法により訓練を行いました(図3b)。また、部分観測時の計測誤差を想定して入力にガウシアンノイズを与え、その大きさによる推定誤差の推移を解析したところ、学習時にも入力に観測ノイズを加えることによってノイズへの頑健性が向上することが明らかになりました。
従来手法との比較では主に三好ら[1,2,3]の結果を参考にしています。同一の部分観測条件において、汎く用いられてきた三次元変分法では平均平方二乗誤差が1.3[K]程度[1,2]、アンサンブルカルマンフィルタ法では0.4-0.8[K]程度となること[1,2,3]が報告されており(いずれも観測ノイズ量σ=1[k])、提案手法が従来手法に対して大きなアドバンテージをもっていることがわかります(Lorenz96モデルを用いての、より定量的な性能比較を付録に示しました)。
本結果から、提案手法を気象シミュレーションのデータ同化に活用することの有効性が示されました。これにより、気象シミュレーションが実世界に対して、より高い精度で同期されることになり、気象予測の精度向上に繋がることが期待されます。
5. まとめおよび今後に向けて
気象予測の原理検証モデルにおいて、深層学習を用いた提案手法がデータ同化の精度向上に有効であることを実証しました。今後は、気象予測に用いられる大規模気象シミュレーションに適用し、気象予測の精度向上への取り組みを本格化していきます。
また、当社のデジタルツイン構想では、日本が高い世界シェアを誇る「多様なセンサ」と「多様な認識/観測対象」それぞれに対応可能な汎用性の高い技術開発を進めてきましたが、本取り組みにおいて当社提案手法が有効であることが実証されました。これからは、センサモダリティの拡充 (カメラ画像、 衛星画像等のイメージセンサ、LiDAR等の光センサや加速度センサ、ジャイロセンサ、温度/湿度センサ、歪センサ等)と認識/観測対象の拡充(街や建造物、自動車や製造物等の工業製品、小型の商業製品等)を通じてあらゆるデータを統合的に取り扱いデジタルツイン構想の実現を目指します。
【富士通株式会社様からのエンドースメント】
当社は、これまで、MinD in a Device社に、コンピューティング環境や気象に関する知見を提供させていただいており、今回このような成果が得られたことを、大変喜ばしく思っております。今後も、MinD in a Device社との協力関係を深め、脳のしくみを用いた次世代型AIによる社会課題解決の実現に貢献していきたいと考えています。
富士通株式会社 テクニカルコンピューティングソリューション事業本部
本部長代理 有山 俊朗
【参考文献】
[1]Miyoshi,Takemasa.Ensemble Kalman filter experiments with a primitive-equation global model. Diss. 2005.
[2]Tsuyuki,Tadashi,and Takemasa Miyoshi. "Recent progress of data assimilation methods in meteorology." Journal of the Meteorological Society of Japan. Ser. II 85 (2007): 331-361.
[3]Miyoshi,Takemasa,and Keiichi Kondo. "A multi-scale localization approach to an ensemble Kalman filter." Sola 9 (2013): 170-173.
付録)提案手法についての詳細
1. 概要
深層学習を用いた提案手法のデータ同化精度をより定量的に検証するため、気象予測の原理検証によく用いられるLorenz 96モデルを対象とし、四次元変分法による同化精度との比較を行いました。
2. Lorenz 96モデルについて
Lorenz 96モデルは40変数の常微分連立方程式で、隣り合う変数同士の関係から一変数の時系列データが決まるというものです。気象シミュレーションの特徴を表現しており、気象予測の原理検証によく用いられています。図4 (a)はLorenz 96モデルにおける各変数の時系列データを可視化したものです。
3. 検証方法および結果
提案手法で用いた深層学習は、その訓練のために教師信号および入力信号が必要となります。今回は、最新時刻における全状態変数を教師信号とし、5個毎もしくは10個毎の間隔で部分観測した変数の時間履歴を入力信号としました。図4(b)が提案手法による推定結果で、図4(a)の特徴が残っていることが分かります。
画像4: https://www.atpress.ne.jp/releases/210287/LL_img_210287_4.png
Lorenz 96 モデルの挙動、および提案手法による最新時刻での全状態変数を推定した結果
図4 (a)Lorenz 96モデルの挙動:横軸は各変数(全40変数)、縦軸は時間で、黄色~紺色は数値の大小を示す。赤枠は部分観測データ(深層学習の入力)を示し、灰色枠はシミュレーションの初期時刻における全40変数の状態(深層学習の教師信号)を表す。(b)提案手法による、最新時刻での全状態変数を推定した結果(RMSE = 1.96)。(a)の真値の特徴が十分に残っており、実用的な範囲に収まっている。
図5 左が観測間隔5個毎での結果、右が10個毎での結果になります。どちらも四次元変分法に対し、提案手法のRMSEが大幅に小さくなっていることが分かります。特に、観測間隔が10個毎となる実際のラジオゾンデ観測に即し(図1参照)、より非線形性の強い条件においてその差は顕著となります。
画像5: https://www.atpress.ne.jp/releases/210287/LL_img_210287_5.png
最新時刻における全変数の推定結果と、真値との誤差をRMSEで表したグラフ
図5 最新時刻における全変数の推定結果と、真値との誤差をRMSEで表したグラフ:(a) 変数の観測間隔を5個毎、右図は10個毎とした時の結果を示し、横軸は観測ノイズ量(分散)、縦軸はRMSEを表す。提案手法における複数の曲線は、訓練ノイズ量(分散)の違いによるものであり、観測ノイズが概ね既知であることから、各観測ノイズ値に対してRMSEが最小となる曲線が提案手法の性能を表すことになる。(b)観測間隔10個毎、すなわち全変数に対し1/10となる4点しか観測できない条件の結果においてその差はより顕著となり、四次元変分法のRMSEが4.5程度とほとんどデータ同化が出来ていないレベルである一方、提案手法は1.5~2.8と実用的な範囲に抑えられている(全変数の推測結果は図4(b)参照)。
【株式会社MinD in a Deviceについて】
社名 : 株式会社MinD in a Device(マインド・イン・ア・デバイス)
URL : https://mindinadevice.com/
本社所在地: 東京都世田谷区
研究実施者: 渡辺 正峰(提案手法の発案およびコーディング)、
菊地 亮太(全体監修、従来手法のコーディング)
【機械学習エンジニア募集ページ】
https://www.wantedly.com/projects/296225
