瞬時に判れば天才!一筆書きの終点を答えよ!
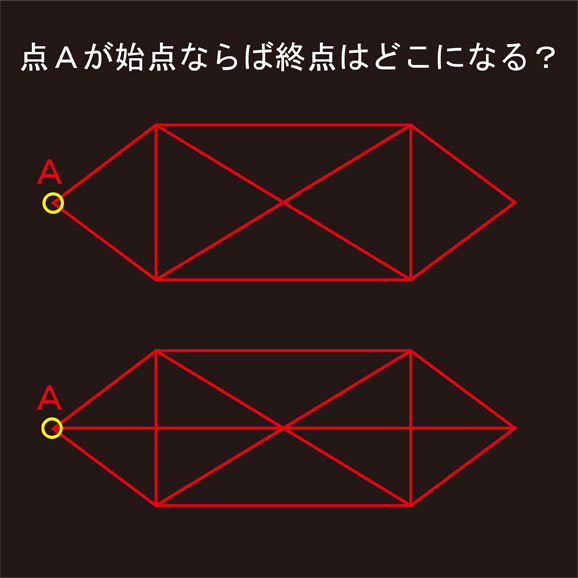
線だけで描かれた図形には色々な形がありますが、それらの図形は一筆書きが出来たり出来なかったりします。この2つの図形はどちらも一筆書きをすることができます。しかし、この問題は一筆書きをする問題ではありません。書き始めの点を黄色の〇印をつけた点Aとするとき、書き終わりの点がどこになるのかを答える問題です。
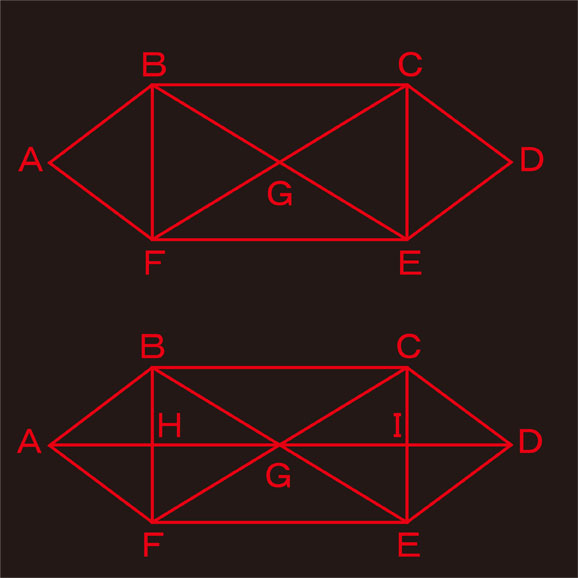
図形の中にある各点(共有点)に記号をつけました。
答えがわかったとしても、このままでは答えることができません。答えやすいように各点に記号をつけました。これでもう答えることができます。実際に、2つの図形を一筆で描いてみると答えをイメージできるかもしれません。しかし、そのイメージが正しいかどうかはわかりません。正しい答えはどのようにして見つけると良いのでしょう。それぞれの点から何本の線が出ているかを数えてみて下さい。
各点からの線の数をまとめると...。
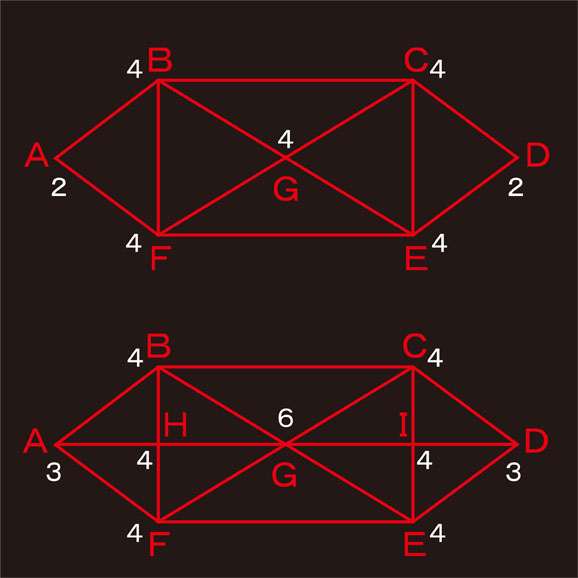
各点から出ている線の数を、それぞれの点の横に書き出してみました。2つの図形を見て気付くことはありませんか。
2つの図形のうち、上側の図形では、各点から出る線の数はすべて偶数本です。しかし、下側の図形では偶数本の場所と奇数本の場所があります。
偶点(偶数点)と奇点(奇数点)
それぞれの点から出ている線の数が偶数である場合、その点のことを偶点(偶数点)といいます。また、出ている線の数が奇数である場合は、その点を奇点(奇数点)といいます。
図形が一筆書きできるかどうかは、その図形の中にある偶点と奇点の数で判断することができます。また、始点が決まっているときに終点の場所もわかります。
上側に描かれていた図形です。
この図形には奇点は1つもありません。すべて偶点です。すべてが偶点である図形は必ず一筆書きをすることができます。どの点から描き始めても必ず一筆書きをすることができて、始点と終点は一致します。
下側に描かれていた図形です。
この図形には奇点が2個あります。奇点が2個だけある図形は一筆書きをすることができます。2個の奇点のうちどちらを始点にしても一筆書きをすることができ、もう一方の奇点が終点となります。奇点が3個以上ある場合には一筆書きをすることはできません。
答です。
ということで、上側の図形では一筆書きの終点は始点と一致します。また、下側の図形では終点は点Dとなります。
一筆書きができる図形は、すべての点が偶点であるか、奇点の個数が2個の場合です。色々な図形を描いて一筆書きの問題を作って見るのも面白いかもしれません。
一筆書きができる図形だとわかっても、あなたが実際に一筆書きをできるかどうかはわかりません。結び目ができるのはどちらだ!一瞬で答えられたら天才! という問題もありました。
